如何计算点到平面的距离

软件教程
1

软件版本：3d slicer 5.2.2
问题描述：利用三点确定了平面，怎么计算平面外一点到平面的距离呢

3

3D Slicer 教程：使用Python计算平面外一点到平面的距离

背景

在医学影像分析中，测量点到平面的距离有时是必不可少的几何分析任务。这个教程将指导您如何在3D Slicer中使用标记点（Fiducials）来确定一个由三个点构成的平面，然后使用Python计算另一个点到该平面的距离。通过这种方式，您可以更方便、快捷地进行几何计算。

教程目标

  • 设置四个标记点，分别命名为F-1、F-2、F-3和F-0。
  • 使用Python脚本获取标记点的坐标。
  • 计算点F-0到由F-1、F-2、F-3构成平面的距离。

步骤1：添加标记点

  1. 加载影像数据
    首先，在3D Slicer中加载您需要分析的影像数据（如脑部MRI或CT图像）。

  2. 进入 Markups 模块
    在模块菜单中，选择 Markups 模块。通过工具栏中的“+ Fiducial”按钮，依次在影像中点击四个位置来添加标记点。

  3. 重命名标记点
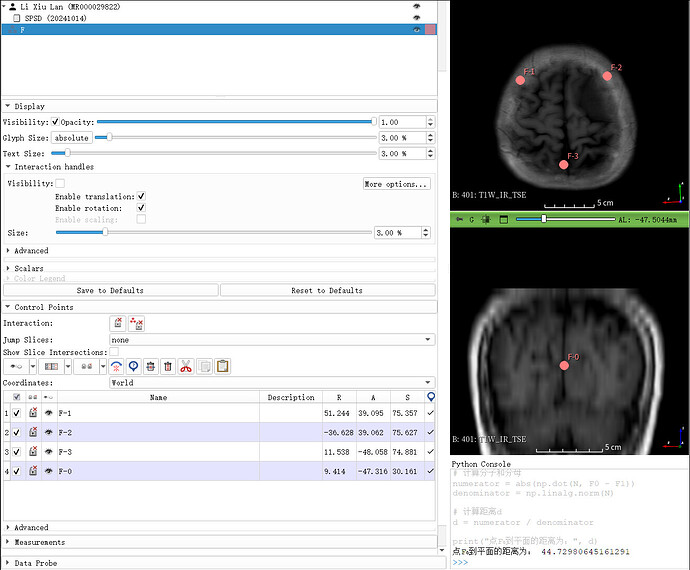
    在 Markups 模块中，找到标记点的列表。您可以通过双击每个标记点的名称，依次将它们重命名为 F-1、F-2、F-3 和 F-0。

    注意：尽管标记点名称中可以包含破折号（如F-1），但在Python代码中，破折号不允许出现在变量名中。因此我们会在代码中处理这个问题。

    标记点的坐标列表如下图所示：

步骤2：打开Python控制台

  1. 在3D Slicer主界面，点击 View → Python Interactor 打开Python控制台。
  2. 控制台将出现在Slicer窗口的底部，供您输入和执行Python代码。

步骤3：编写和运行Python代码

将以下Python代码复制到控制台中，然后按回车键运行：

import numpy as np
import slicer

# 获取标记点节点（默认为“F”，根据实际进行修改）
fiducialNode = slicer.util.getNode('F')

# 初始化一个字典来存储点的坐标
points = {}

# 获取标记点的数量
numFiducials = fiducialNode.GetNumberOfControlPoints()

# 遍历所有标记点，获取其标签和坐标
for i in range(numFiducials):
    label = fiducialNode.GetNthControlPointLabel(i)
    pos = [0.0, 0.0, 0.0]
    fiducialNode.GetNthControlPointPosition(i, pos)
    # 替换掉破折号以便在代码中使用
    label = label.replace('-', '')
    points[label] = np.array(pos)

# 检查是否成功获取所有需要的点
required_points = ['F1', 'F2', 'F3', 'F0']
for pt in required_points:
    if pt not in points:
        raise ValueError(f"未找到标记点 {pt}，请确保已正确命名。")

# 提取点的坐标
F1 = points['F1']
F2 = points['F2']
F3 = points['F3']
F0 = points['F0']

# 计算向量A和B
A = F2 - F1
B = F3 - F1

# 计算法向量N
N = np.cross(A, B)

# 计算分子和分母
numerator = abs(np.dot(N, F0 - F1))
denominator = np.linalg.norm(N)

# 计算距离d
d = numerator / denominator

print("点F₀到平面的距离为：", d)

步骤4：查看结果

当代码成功执行后，Python控制台将输出点F-0到由F-1、F-2和F-3构成的平面的距离。结果显示为一个浮点数，表示该点到平面的直线距离，单位与影像数据一致（通常是毫米）。

代码解释

  1. 获取标记点节点：

    • 使用 slicer.util.getNode('F') 获取名为 F 的标记点节点，该节点包含了您在影像上放置的所有标记点。

  2. 处理标记点标签：

    • 由于标记点可能命名为 F-1、F-2 等，但Python不允许变量名中含有破折号，因此使用 label.replace('-', '') 将破折号替换为空字符串。这样，标记点名称在代码中将变为 F1、F2、F3 和 F0。

  3. 计算向量和法向量：

    • A = F2 - F1 和 B = F3 - F1 分别表示从 F1 到 F2 和 F1 到 F3 的向量。
    • np.cross(A, B) 计算这两个向量的叉积，得到平面的法向量 N。

  4. 计算点到平面的距离：

    • 使用点到平面距离的标准公式：
      [
      d = \frac{|N \cdot (F₀ - F₁)|}{||N||}
      ]
      其中 |N \cdot (F₀ - F₁)| 表示法向量 N 与从 F1 指向 F0 向量的点积的绝对值，||N|| 为法向量的模。

  5. 输出结果：

    • 结果为一个浮点数，表示点 F-0 到由 F-1、F-2 和 F-3 构成平面的距离。

常见问题

  1. 为什么标记点名不能包含破折号？
    在Python中，破折号 - 用作减号运算符，因此不能作为变量名的一部分。如果您希望标记点名中有破折号，可以在代码中将它替换掉，以确保Python能够正确处理。

  2. 如何确保坐标单位一致？
    3D Slicer中的坐标单位通常与影像数据一致。如果您处理的是医学影像数据，单位通常是毫米（mm）。确保在计算中所有的标记点都使用相同的单位。

总结

通过本教程，您学会了如何在3D Slicer中设置标记点，并通过Python脚本计算点到平面的距离。这种方法可以帮助您在医学影像分析中快速进行几何计算。您还可以根据需求，扩展该脚本来计算其他几何特征。